THIS is MY folDEr: MATEMATHICA

LOGARITMA

Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.

Rumus dasar logaritma:

Mencari nilai logaritma:
Cara untuk mencari nilai logaritma antara lain dengan menggunakan:
* Tabel
* Kalkulator (yang sudah dilengkapi fitur log)

Kegunaan logaritma:
Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial.

Rumus Logaritma:

Sains dan teknik:
Dalam sains, terdapat banyak besaran yang umumnya diekspresikan dengan logaritma. Sebabnya, dan contoh-contoh yang lebih lengkap, dapat dilihat di skala logaritmik.

* Negatif dari logaritma berbasis 10 digunakan dalam kimia untuk mengekspresikan konsentrasi ion hidronium (pH). Contohnya, konsentrasi ion hidronium pada air adalah 10−7 pada suhu 25 °C, sehingga pH-nya 7.

* Satuan bel (dengan simbol B) adalah satuan pengukur perbandingan (rasio), seperti perbandingan nilai daya dan tegangan. Kebanyakan digunakan dalam bidang telekomunikasi, elektronik, dan akustik. Salah satu sebab digunakannya logaritma adalah karena telinga manusia mempersepsikan suara yang terdengar secara logaritmik. Satuan Bel dinamakan untuk mengenang jasa Alexander Graham Bell, seorang penemu di bidang telekomunikasi. Satuan desibel (dB), yang sama dengan 0.1 bel, lebih sering digunakan.

* Skala Richter mengukur intensitas gempa bumi dengan menggunakan skala logaritma berbasis 10.

* Dalam astronomi, magnitudo yang mengukur terangnya bintang menggunakan skala logaritmik, karena mata manusia mempersepsikan terang secara logaritmik.

Penghitungan yang lebih mudah:
Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:

Sifat-sifat diatas membuat penghitungan dengan eksponen menjadi lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum tersedianya kalkulator sebagai hasil perkembangan teknologi modern.

Untuk mengkali dua angka, yang diperlukan adalah melihat logaritma masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog jumlah tersebut dalam tabel. Untuk mengitung pangkat atau akar dari sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel, lalu hanya mengkali atau membagi dengan radix pangkat atau akar tersebut.

Kubus dan Balok

Kubus dan balok merupakan bangun ruang yang terbentuk dari susunan bangun datar.
KUBUS, merupakan bangun ruang yang terdiri dari persegi yang kongruen (sama besar).

kubus

BALOK, merupakan bangun ruang yang dapat terdiri dari persegi ataupun persegi panjang. Bangun tersebut sama panjang dengan dihadapannya.

balok

Rusuk
Rusuk ialah ruas garis pada kubus dan balok, terdapat 12 rusuk. Pada kubus rusuk yang dimiliki sama panjang namun pada balok rusuk yang sejajar saja yang memiliki panjang yang sama. Contoh:
Rusuk alas : AB, BC, CD, AD
Rusuk tegak : AE, BF, CG, EH
Rusuk atap : EF, FG, GH, EH
Bidang / sisi
Bidang/sisi adalah bagun datar yang memisahkan antara bagian dalam dan bagian luar. Banyaknya sisi yang dimilikinya sebanyak enam sisi.
Sisi alas : ABCD
Sisi atas : EFGH
Sisi kanan : BCGF
Sisi kiri : ADHF
Sisi depan : ABFE
Sisi belakang : CDHG

Titik sudut
Terdapat 8 titik sudut pada bangun ini. Penamaan titik sudut ini menggunakan huruf capital, titik sudut merupakan pertemuan 3 rusuk yang bertemu pada satu titik. Yaitu: A, B, C, D, E, F, G, H.

Diagonal sisi
Diagonal sisi adalah ruas garis yang terbentuk oleh sudut yang berhadapan pada satu bidang. Ada 12 diagonal sisi, hal ini didapat karena pada kubus dan balok mempunyai 6 bidang/sisi masing-masing bidang tersebut memiliki 2 sudut yang berhapan maka didapatkanlah 2 diagonal sisi, maka 2 x 6 (banyaknya sisi) = 12.
Contoh: AC, BD, AF, BE, dll.

Diagonal ruang
Diagonal ruang adalah ruas garis yang terbentuk oleh sudut yang berhadapan pada satu ruang. Terdapat 4 diagonal ruang, yaitu: AG, BH, CE, DF.

Bidang diagonal
Terdapat 6 bidang diagonal pada kubus dan balok. Bidang diagonal ini terdapat pada bagian dalam yang berbentuk persegi panjang, yaitu: ACGE, BFHD, BCHE, ADGF, dll.

RUMUS KUBUS DAN BALOK
Volume kubus:
V = s x s x s
= s³
Panjang rusuk:
P rusuk = 12 x s
= 12s
Luas kubus/luas permukaan kubus:
L = 6 x s²
= 6s²
Volume balok:
V = panjang x lebar x tinggi
= p x l x t
Panjang rusuk:
P rusuk = 4p + 4l + 4t
= 4 (p + l + t)
Luas balok/luas permukaan balok
L = 2pl + 2pt + 2lt
= 2(pl + pt + lt)
Lingkaran

A. Persamaan Lingkaran yang berpusat di O (0, 0) dan berjari-jari r.

Dari gambar, diperoleh persamaan : OP = r

Sehingga diperoleh persamaan lingkaran dengan pusat di O dan berjari-jari r , yaitu :

Suatu titik A

dikatakan :
a. Terletak pada lingkaran

b. Terletak di dalam lingkaran

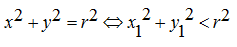
c. Terletak di luar lingkaran

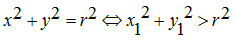
B. Persamaan Lingkaran yang berpusat di P (a, b) dan berjari-jari r.

Gambar di atas adalah sebuah lingkaran dengan pusat (a, b) dan berjari-jari r. Titik Q (x, y) adalah sebuah titik pada lingkaran.
Dari gambar diperoleh persamaan : PQ = r

Sehingga diperoleh persamaan lingkaran dengan pusat di P (a, b) dan berjari-jari r, yaitu :

Suatu titik A

dikatakan :
a. Terletak pada lingkaran

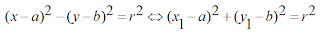
b. Terletak di dalam lingkaran

c. Terletak di luar lingkaran

C. Persamaan Umum Lingkaran
Bila kita menjabarkan persamaan :

Dan mengatur kembali suku-sukunya, maka akan diperoleh :

Persamaan terakhir dapat pula dinyatakan dengan :

Dengan :

Persamaan (3) merupakan persamaan lingkaran dengan pusat di

dan berjari-jari

D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
* Garis singgung lingkaran melalui sebuah titik pada lingkaran